В школу я ненавидела математику.Это было тяжелое, сухие и скучные вещи с душным старых книг и очень теоретических проблем.Хуже того, многие задачи были повторными, с простым логическим изменением в каждой итерации (деления чисел стороны, дифференциалы и т.д.).Именно по этой причине мы изобрели компьютеры.Достаточно сказать, многие мои математике домашнее задание было фактически сделано мой верный Commodore 64 и некоторые линии Basic, со мной просто скопировав результаты позже on.

Эти инструменты и несколько уроков геометрии я дал мне время и вдохновение, чтобы сделать математику интересной для себя.Я сделал это, в первую очередь, путем создания визуальных эффектов, которые следуют правилам математического В демо, интро и другие, казалось бы бессмысленным things.

Существует много математики в визуальном, что мы делаем, даже если мы этого не осознаем.Если вы хотите сделать что-то выглядеть естественно и двигаться естественно, нужно добавить немного физики и округления до этого.Природа не работает в прямых углов или линейного ускорения.Вот почему зомби в фильмах так жутко.Это был покрытые здесь раньше по отношению к CSS animation, но сегодня давайте немного глубже и посмотреть на простой математике за гладкую looks.

Поездка от 0 до 1 Без Будучи Boring

Если вы только начали программирования и просят, чтобы перейти от 0 до 1 с в нескольких шагах между ними, вы, вероятно, пойти на for цикл:

for ( i = 0; i <= 1; i += 0.1 ) {
  x = i;
  y = i;
…
}

Это приведет линия на графике, что составляет 45 градусов.Ничто в природе не движется с этой точностью:

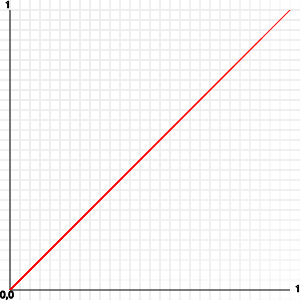
Простой способ сделать это движение немного более естественным было бы просто умножить значение сама по себе:

for ( i = 0; i <= 1; i += 0.1 ) {
  x = i;
  y = i * i;
}

Это означает, что 0.1 0.01 0.2 составляет 0.04 0.3 составляет 0.09 0.4 составляет 0.16 0.5 составляет 0.25 и так далее.В результате кривая, которая начинается плоская, а затем становится круче к концу:

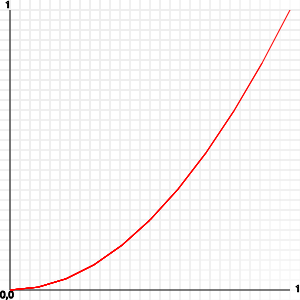
Вы можете сделать это еще более выраженным, продолжая размножаться или с помощью “к власти” Math.pow() функции:

for ( i = 0; i <= 1; i += 0.1 ) {
  x = i;
  y = Math.pow( i, 4 );
}

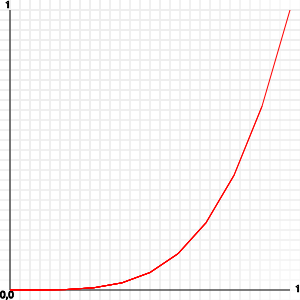
Это один из приемов ослабление функций, используемых в библиотеках, таких как JQuery и YUI, а также в CSS переходов и анимации в современном browsers.

Вы можете использовать эту же способом, но есть еще более простой вариант для получения значения между 0 и 1, что следующим естественным motion.

Не грех,Просто природного Motion

Синус waves являются, пожалуй, лучшее, что когда-либо для плавной анимации.Они происходят в природе: свидетель весной с весом на это, океанские волны, звук и свет.В нашем случае, мы хотим двигаться от 0 до 1 smoothly.

Чтобы создать движение, которое идет от 0 к 1 и обратно до 0 гладко, мы можем использовать синусоидальную волну, которая идет от 0 до π в несколько шагов.Полный синусоидальной волны происходит от 0 до π × 2 (т. е. целый круг) приведет значений от -1 до 1, и мы не хотим, что (пока)

var counter = 0;

// 100 iterations
var increase = Math.PI / 100;

for ( i = 0; i <= 1; i += 0.01 ) {
  x = i;
  y = Math.sin(counter);
  counter += increase;
}

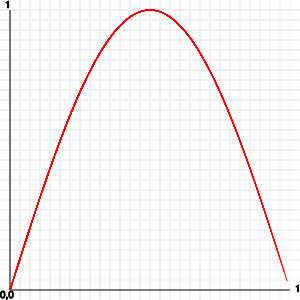
быстрый сторону на номера синус и косинус: И Math.sin() и Math.cos() принимать в качестве параметра угол, что должно быть в radians.Как люди, тем не менее, градус в диапазоне от 0 до 360 гораздо легче читать.Вот почему можно и нужно конвертировать между ними с этой простой формуле:

var toRadian = Math.PI / 180;
var toDegree = 180 / Math.PI;

var angle = 30;

var angleInRadians = angle * toRadian;
var angleInDegrees = angleInRadians * toDegree;

Вернуться на нашем синусоиды.Вы можете играть с этим много.Например, вы можете использовать абсолютное значение полного 2 × π цикла:

var counter = 0;
// 100 iterations
var increase = Math.PI * 2 / 100;

for ( i = 0; i <= 1; i += 0.01 ) {
  x = i;
  y = Math.abs( Math.sin( counter ) );
  counter += increase;
}

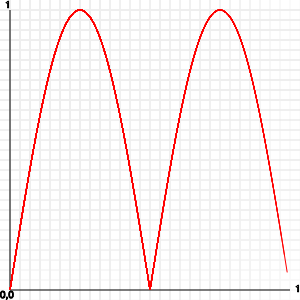
Но опять же, это выглядит грязным.Если вы хотите полную вверх и вниз, без перерыва в середине, то вам нужно перенести значения.Вы должны половину синуса, а затем добавить 0,5 до него:

var counter = 0;
// 100 iterations
var increase = Math.PI * 2 / 100;

for ( i = 0; i <= 1; i += 0.01 ) {
  x = i;
  y = Math.sin( counter ) / 2 + 0.5;
  counter += increase;
}

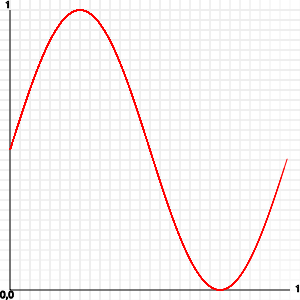
Итак, как вы можете использовать это?Имея функцию, которая возвращает -1 до 1, чтобы все, что вы кормите его может быть очень прохладно.Все, что вам нужно сделать, это умножить на значения, которые вы хотите, и добавить смещение, чтобы избежать негативных numbers.

Например, проверить синус этого движения demo:

Выглядит аккуратно, не так ли?Много обмана уже в CSS:

.stage {
  width:200px;
  height:200px;
  margin:2em;
  position:relative;
  background:#6cf;
  overflow:hidden;
}

.stage div {
  line-height:40px;
  width:100%;
  text-align:center;
  background:#369;
  color:#fff;
  font-weight:bold;
  position:absolute;
}

stage элемент имеет фиксированный размер и позиционируется относительно.Это означает, что все, что расположено внутри абсолютно это будет по отношению к элементу itself.

Дел внутри этапа 40 пикселей в высоту и позиционируется абсолютно.Теперь все, что нам нужно сделать, это переместить блок с JavaScript в синусоиду:

var banner = document.querySelector( '.stage div' ),
    start = 0;
function sine(){
  banner.style.top = 50 * Math.sin( start ) + 80 + 'px';
  start += 0.05;
}
window.setInterval( sine, 1000/30 );

Начало изменении значения постоянно, и с Math.sin() получаем хорошие движения волны.Умножим это на 50, чтобы получить более широкую волну, и мы добавим 80 пикселей в центре его находится в стадии элемента.Да, элемент 200 пикселей в высоту и 100 в два раза меньше, но потому, чтоБаннер в 40 пикселей в высоту, мы должны вычесть половину, что в центре it.

Прямо сейчас, это просто вверх-вниз движения.Ничто не мешает вам, хотя, с делая его более интересным.Множитель 50, например, может быть синусоида себя с другим значением:

var banner = document.querySelector( '.stage div' ),
    start = 0,
    multiplier = 0;
function sine(){
  multiplier = 50 * Math.sin( start * 2 );
  banner.style.top = multiplier * Math.sin( start ) + 80 + 'px';
  start += 0.05;
}
window.setInterval( sine, 1000/30 );

результат this есть баннер, который, кажется, предварительно двигаться вверх и вниз.Назад в день и на очень медленном Commodore 64, расчета синусоиды живая была слишком медленной.Вместо этого, мы должны были инструменты для создания таблиц синуса (массивы, если хотите), и мы построили те, кто непосредственно.Одним из инструментов для создания большой синусоиды, так что вы могли бы подпрыгивая выделите текст был Wix Bouncer:

Круги на песке, кругом …

Круговое движение является вещь красоты.Это радует глаз, напоминает нам о прялки и землю мы стоим на, и в целом имеет “это не компьютер вещи” чувство к нему.Математика что-то замышляет по кругу не hard.

Она восходит к Pythagoras, который, как по слухам, привлек много круги на песке, пока не нашел своего знаменитого theorem.Если вы хотите использовать все хорошие вещи, которая приходит из этой теоремы, а затем попытаться найти треугольник с прямым углом.Если гипотенуза этого треугольника равен 1, то вы можете легко рассчитать горизонтальное ногу, как косинус угла и вертикальной ноги, как синус угла:

Как это, относящихся к кругу?Ну, это довольно просто найти прямоугольного треугольника в круг, чтобы все его точки:

Это означает, что если вы хотите построить что-то на круг (или сделать один), вы …

Если вы хотите прочитать полностью статью, посетите сайт наших спонсоров